6% Better Math Reasoning in Fewer Tokens: Multiplex Thinking Merges Multiple Paths into One
Standard chain-of-thought commits to one token at a time, like depth-first search through a maze.
Chain-of-thought reasoning has become the standard approach for complex problem solving in large language models, but it comes with a fundamental limitation: each token commits the model to a single reasoning path. Building on continuous reasoning approaches like Soft Thinking [1] and COCONUT [2], researchers from the University of Pennsylvania and Microsoft Research introduce Multiplex Thinking, a method that samples multiple candidate tokens at each step and merges them into a single continuous representation. This allows the model to explore multiple reasoning paths simultaneously without increasing sequence length.
The key insight addresses a critical gap in existing work. Continuous token approaches like Soft Thinking effectively compress reasoning information but are deterministic, making all rollouts identical and preventing the exploration needed for reinforcement learning. Multiplex Thinking bridges this gap by preserving stochastic sampling dynamics while operating in a continuous space.
How Multiplex Thinking Works
At each reasoning step, instead of committing to a single discrete token, Multiplex Thinking independently samples K tokens from the model's probability distribution. These tokens are then aggregated into a single continuous "multiplex token" by averaging their one-hot vectors and mapping through the embedding matrix.
The mechanism is self-adaptive. When the model is confident and the probability distribution is peaked, the K samples tend to coincide, and the multiplex token behaves like a standard discrete token. When uncertainty is high and exploration is valuable, the samples diverge, encoding multiple plausible reasoning paths within a single continuous vector.
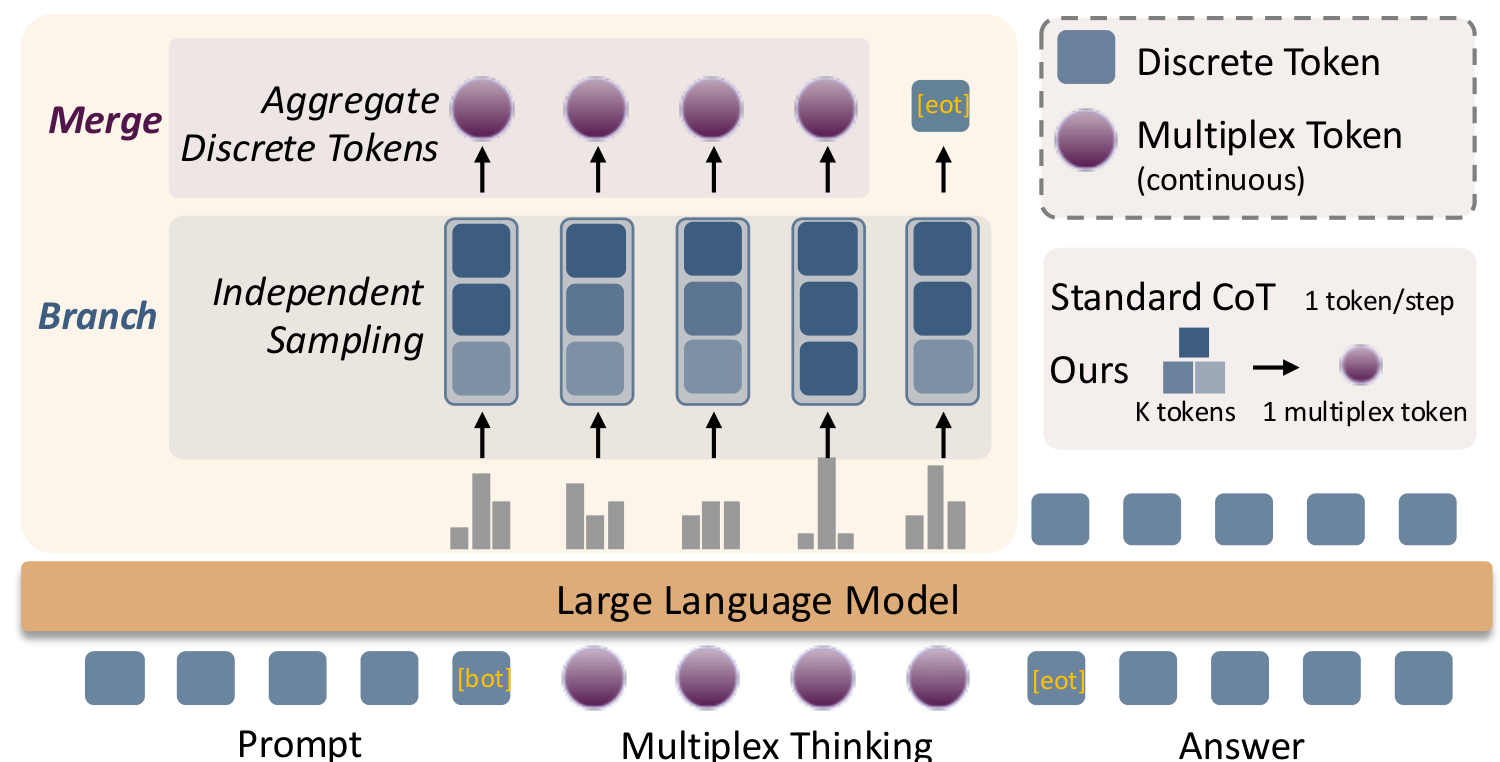Multiplex ArchitectureThe branch-and-merge mechanism samples K independent tokens and aggregates them into a single continuous multiplex token, enabling breadth-first exploration within each step.
The probability of generating a specific multiplex token factorizes due to the independence of the K samples. This factorization is crucial because it allows the entire reasoning trajectory to have a tractable probability distribution, enabling direct optimization with on-policy reinforcement learning.
Training with Reinforcement Learning
Unlike deterministic continuous approaches that collapse the policy distribution, Multiplex Thinking's stochastic formulation is directly compatible with RL objectives. The method uses Group Relative Policy Optimization (GRPO) [6] to train the model, maximizing the expected reward over generated answers. Training was conducted on the DeepScaleR-Preview-Dataset, which contains approximately 40,000 unique mathematical problem-answer pairs.
The training objective optimizes the joint generation of the multiplex thinking trace and the final answer. Because each multiplex token's probability is simply the product of its K sampled tokens' probabilities, the log-probability of the entire trajectory decomposes cleanly into a sum over all samples.
The thinking phase terminates when the highest-probability token becomes the special end-of-thinking token. The authors explicitly avoid heuristics like monitoring for consecutive low-entropy tokens, finding that such patterns can be exploited during RL training.
Notably, the method also works at inference time without training. The inference-only variant, Multiplex Thinking-I, outperforms Discrete CoT on the 7B model, achieving better results on four out of six benchmarks without any RL fine-tuning. This demonstrates that the intrinsic capabilities of multiplex representation benefit reasoning even before optimization.
Experimental Results
Multiplex Thinking was evaluated on six challenging mathematical reasoning benchmarks using DeepSeek-R1-Distill-Qwen models at 1.5B and 7B parameter scales. The method achieves best Pass@1 performance in 11 out of 12 evaluation settings.
On the 7B model, Multiplex Thinking achieves 20.6% on AIME 2024 compared to 17.2% for Discrete RL and 15.7% for Discrete CoT. On MATH-500, it reaches 78.0% versus 74.1% for Discrete RL. The gains are consistent across AMC 2023 (50.7% vs 44.7%), Minerva (38.6% vs 35.3%), and OlympiadBench (41.7% vs 38.0%).
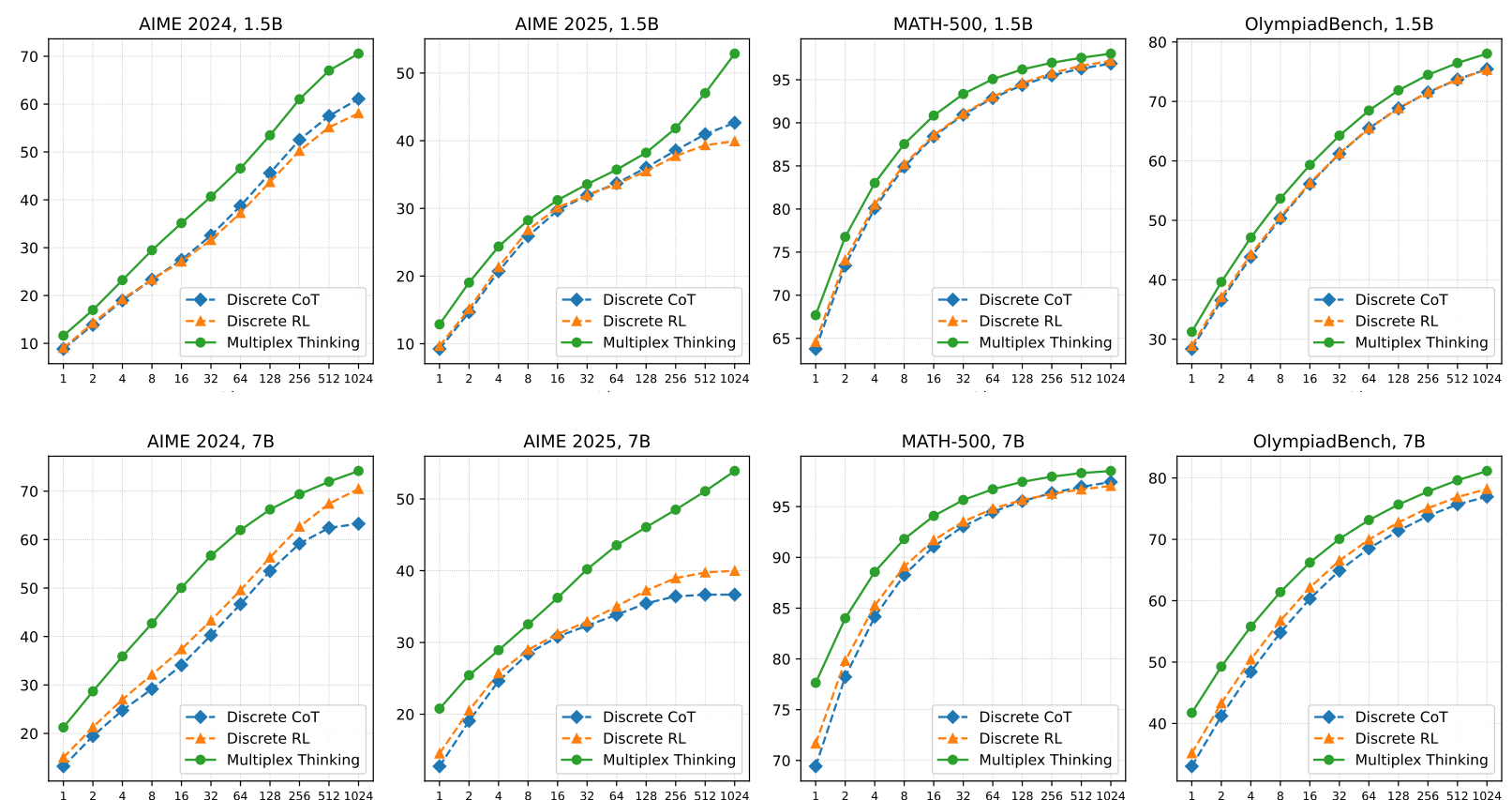Pass@k ResultsMultiplex Thinking consistently outperforms discrete baselines from Pass@1 through Pass@1024, with widening gaps on challenging tasks like AIME where exploration matters most.
The exploration advantages become more pronounced at higher Pass@k values. On AIME 2025 with the 7B model, while Discrete RL plateaus around 40% at Pass@1024, Multiplex Thinking continues scaling to approximately 55%. This 15 percentage point gap suggests the continuous representation effectively expands the viable search space.
Token Efficiency
Beyond accuracy improvements, Multiplex Thinking generates shorter responses. Training dynamics show the method consistently produces trajectories with 3200-3400 tokens compared to 3600-3800 for Discrete RL, representing 10-15% shorter sequences while achieving higher accuracy.
This efficiency stems from the higher information density of multiplex tokens. Since each token encodes multiple potential paths, complex reasoning steps can be expressed more compactly. The inference-only variant Multiplex Thinking-I with a 4k token budget actually outperforms Discrete CoT with 5k tokens (40.5% vs 39.6% averaged across benchmarks), demonstrating that performance gains can be achieved through richer token representations rather than longer sequences.
Analysis of Multiplex Width
The impact of the multiplex width K reveals important insights. Transitioning from K=1 (standard discrete) to K=2 yields substantial gains across all benchmarks. On AMC 2023, accuracy jumps from 44.7% to 49.6%. However, marginal returns diminish: moving from K=2 to K=3 provides smaller improvements, and K=3 to K=6 shows even less difference.
The entropy analysis provides a theoretical explanation. The entropy of a multiplex token scales linearly with K, corresponding to an exponential expansion of the effective exploration volume from |V| to |V|^K. Multiplex training exhibits 38-40% less entropy collapse than discrete RL, suggesting better sustained exploration throughout training.
Research Context
This work builds on Soft Thinking [1], which introduced probability-weighted embedding mixtures for continuous reasoning, and COCONUT [2], which pioneered hidden-state continuous thoughts. Unlike these deterministic approaches, Multiplex Thinking's stochastic formulation enables RL optimization while maintaining exploration capability.
What's genuinely new:
- Stochastic sampling-based continuous tokens that preserve discrete dynamics while enabling RL
- Tractable probability factorization over multiplex rollouts
- Self-adaptive behavior that collapses to discrete when confident and encodes diversity when uncertain
Compared to Stochastic Soft Thinking [3], which injects Gumbel noise to enable exploration, Multiplex Thinking's independent K-sampling provides the tractable probability structure needed for direct on-policy optimization. The method is best suited when training compute is available for RL fine-tuning and verifiable rewards exist.
Open questions:
- Does the method transfer to non-mathematical reasoning tasks?
- What is the computational overhead of K sampling during training and inference?
- Can adaptive K selection improve efficiency by using smaller K when confident?
Limitations
The evaluation is limited to mathematical reasoning benchmarks, leaving generalization to other domains uncertain. The experiments use only 1.5B and 7B models, with larger scale experiments missing. The authors note that larger model capacity appears essential for resolving interference between superposed reasoning paths.
Check out the Paper and GitHub. All credit goes to the researchers.
References
[1] Zhang, Z. et al. (2025). Soft Thinking: Unlocking the Reasoning Potential of LLMs in Continuous Concept Space. arXiv preprint. arXiv
[2] Hao, S. et al. (2025). Training Large Language Models to Reason in a Continuous Latent Space. arXiv preprint. arXiv
[3] Wu, J. et al. (2025). LLMs are Single-Threaded Reasoners: Demystifying the Working Mechanism of Soft Thinking. arXiv preprint. arXiv
[4] Guo, D. et al. (2025). DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. Nature. arXiv
[5] Wei, J. et al. (2022). Chain of Thought Prompting Elicits Reasoning in Large Language Models. NeurIPS 2022. arXiv
[6] Shao, Z. et al. (2024). DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models. arXiv preprint. arXiv
