Why Hyper-Connections Explode at Scale: DeepSeek's Manifold Fix
Hyper-Connections promised to improve LLMs by expanding the residual stream, but they introduced catastrophic training instability.
The residual connection has remained unchanged since ResNet [2] established it nearly a decade ago. While attention mechanisms evolved from self-attention to MLA to GQA, the simple identity skip connection persisted: add the layer output to the input, and move on. Hyper-Connections (HC) [1] challenged this paradigm by expanding the residual stream width and introducing learnable mappings between features at different depths. The performance gains were substantial, but a critical problem emerged: at scale, HC causes training instability with loss surges and exploding gradients.
Researchers from DeepSeek-AI introduce Manifold-Constrained Hyper-Connections (mHC), a framework that fixes the instability problem through an elegant mathematical constraint. By projecting the residual mappings onto the Birkhoff polytope, a manifold of doubly stochastic matrices, mHC restores the identity mapping property that made residual connections stable in the first place. The result: three orders of magnitude reduction in signal amplification, enabling stable training at 27B parameters with only 6.7% overhead.
The Stability Problem
To understand why HC fails at scale, consider what happens when signals propagate through many layers. In standard residual connections, the identity mapping ensures that signals from shallow layers reach deep layers unchanged. The math is simple: x_L = x_l + sum of layer outputs.
HC replaces the identity with a learnable n x n matrix H_res at each layer. These matrices mix information across the expanded residual streams, enabling richer feature interactions. However, when you multiply these matrices across 60+ layers, the composite mapping can amplify or attenuate signals without bound. DeepSeek's experiments on 27B models show the "Amax Gain Magnitude" reaching 3000, meaning signals can be amplified 3000x as they traverse the network. This leads to gradient explosions, loss surges around 12k training steps, and unstable optimization.
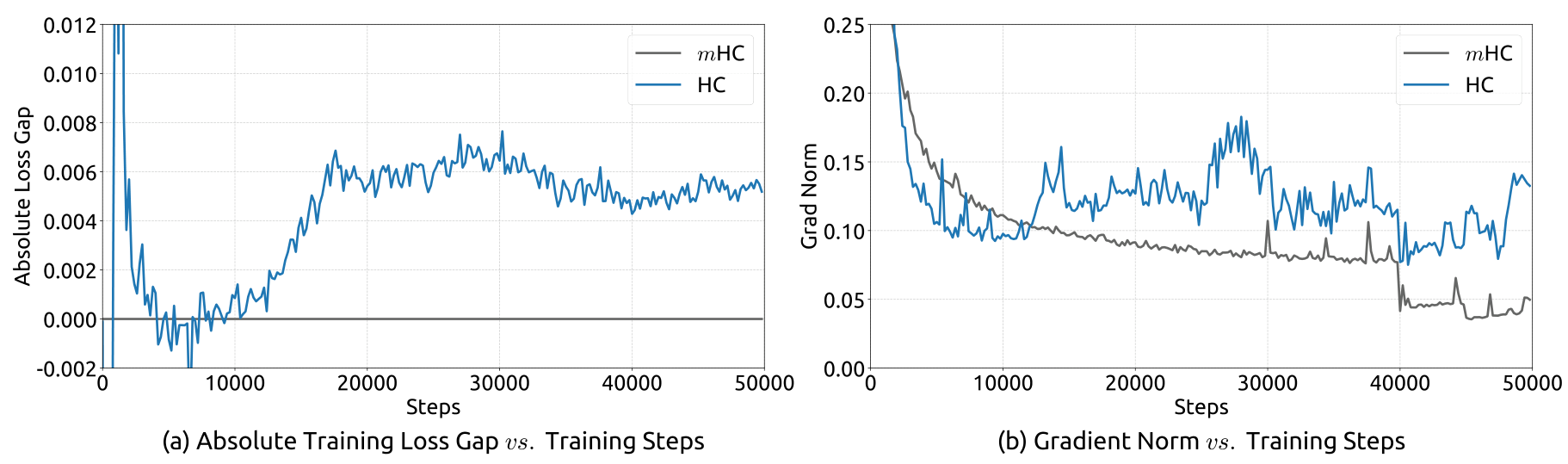HC Training InstabilityTraining loss gap and gradient norm comparison between HC and mHC on 27B models, showing HC's instability spike around 12k steps.
The Manifold Solution
The key insight of mHC is that the problem isn't the expanded residual stream itself; it's the unconstrained nature of the mapping matrices. If H_res could be constrained to never amplify signals, stability would be preserved while maintaining the expressivity benefits.
The solution: constrain H_res to be a doubly stochastic matrix, where both rows and columns sum to 1 and all entries are non-negative. This constraint has three critical properties:
- Norm Preservation: The spectral norm is bounded by 1, so the mapping is non-expansive
- Compositional Closure: The product of doubly stochastic matrices remains doubly stochastic
- Geometric Interpretation: The mapping acts as a convex combination of permutations
The third property is particularly elegant: the set of doubly stochastic matrices forms the Birkhoff polytope, which is the convex hull of all permutation matrices. This means mHC learns a weighted average of different ways to route information across streams, inherently preventing signal explosion.
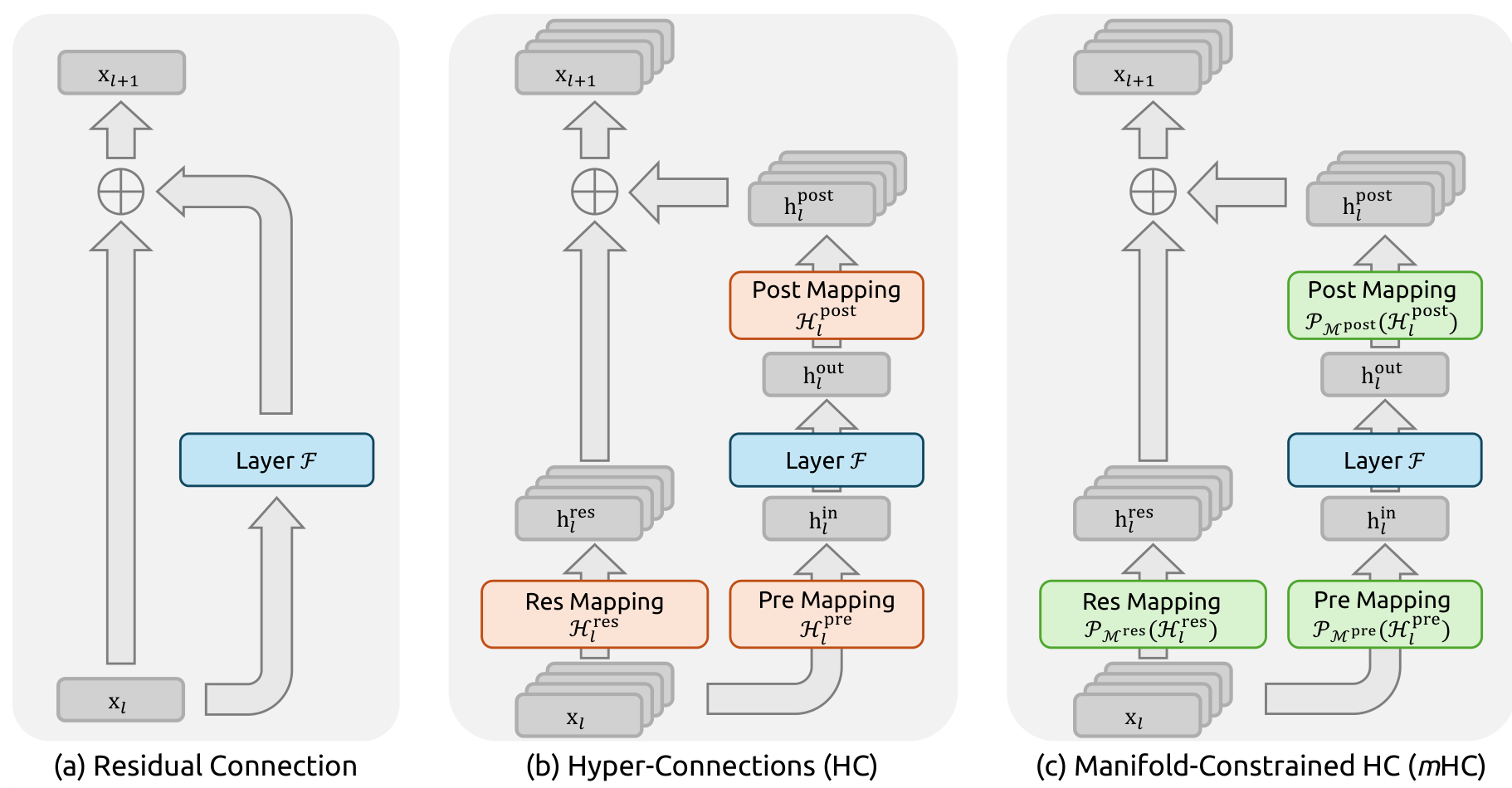Architecture ComparisonSide-by-side comparison of standard residual connection, unconstrained Hyper-Connections (HC), and mHC with manifold projections.
Implementation: Sinkhorn-Knopp Projection
Converting an arbitrary matrix to doubly stochastic form uses the Sinkhorn-Knopp algorithm [7], which alternates between row normalization and column normalization. Starting with M(0) = exp(H_res_raw), the iteration proceeds: M(t) = normalize_rows(normalize_cols(M(t-1))). After 20 iterations, the matrix converges to a doubly stochastic approximation.
For efficiency, mHC includes several infrastructure optimizations built on DeepSeek's DualPipe framework [4]:
- Fused kernels using TileLang for mixed-precision computation
- Selective recomputation that discards intermediate activations in forward pass and recomputes them during backward pass
- Communication overlap in pipeline parallelism to hide the n-fold increase in cross-stage data transfer
These optimizations bring the total training time overhead to just 6.7% for expansion rate n=4.
Results
The stability improvement is dramatic. While HC's Amax Gain Magnitude reaches nearly 3000, mHC stays bounded around 1.6, a three-orders-of-magnitude reduction. This translates to stable gradient norms throughout training, matching the stability profile of standard residual connections.
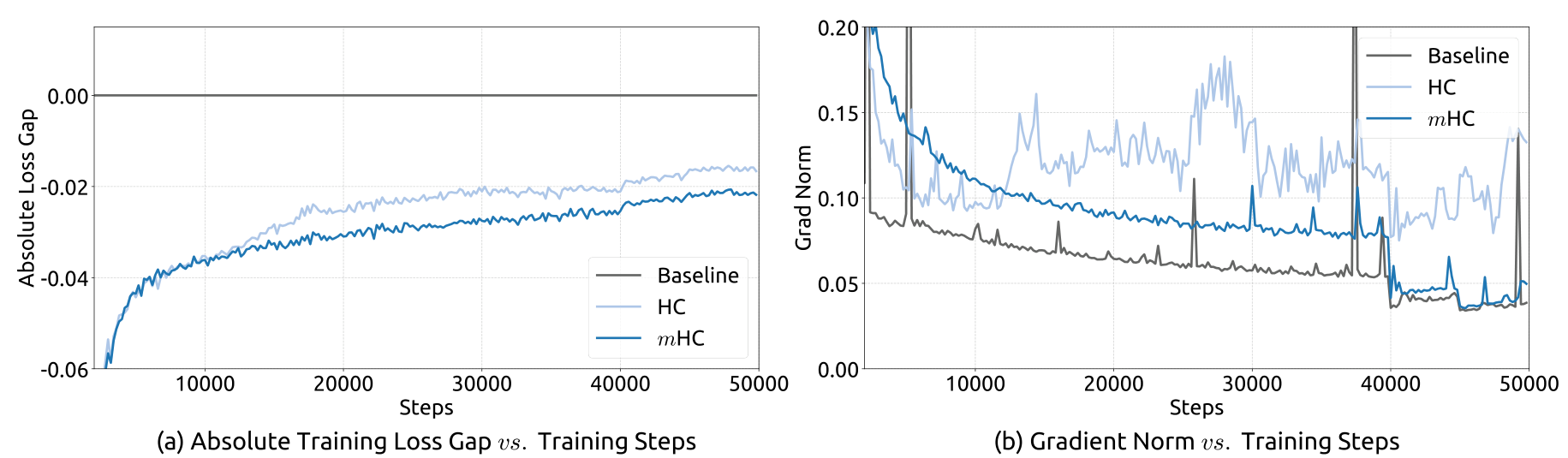Stability ComparisonTraining stability showing mHC's consistent loss curve and gradient norm versus baseline and HC on 27B models.
On downstream benchmarks, mHC demonstrates consistent improvements over both the baseline and original HC:
| Benchmark | Baseline | HC | mHC | |-----------|----------|-----|------| | BBH (3-shot) | 43.8% | 48.9% | 51.0% | | DROP (F1) | 47.0 | 51.6 | 53.9 | | GSM8K | 46.7% | 53.2% | 53.8% | | MMLU | 59.0% | 63.0% | 63.4% |
The improvements are especially notable on reasoning tasks: BBH improves 2.1% over HC and 7.2% over baseline, while DROP shows 2.3% and 6.9% gains respectively.
Benchmark ResultsSystem-level benchmark comparison of Baseline, HC, and mHC across 8 diverse downstream tasks.
Research Context
This work builds directly on Hyper-Connections [1] and the identity mapping principles established by He et al. [3]. The DualPipe schedule and MoE infrastructure come from DeepSeek-V3 [4].
What's genuinely new:
- Application of Sinkhorn-Knopp algorithm to constrain neural network residual mappings
- Formal analysis connecting doubly stochastic constraint to training stability via norm bounds
- Integration of manifold constraints with large-scale distributed training infrastructure
Compared to MUDDFormer [5], which uses dynamic position-dependent connections without stability guarantees, mHC provides provable bounds on signal amplification. MUDDFormer offers more flexibility with minimal overhead (0.4%), making it suited for moderate-scale training, while mHC targets stability-critical large-scale scenarios with its 6.7% overhead.
Open questions:
- Could alternative manifold constraints (orthogonal matrices, semi-orthogonal) provide different tradeoffs?
- Can Sinkhorn-Knopp iterations be made adaptive based on convergence?
- How do manifold constraints interact with other recent innovations like MLA and MoE routing?
Limitations
The authors acknowledge several limitations. The fixed 20-iteration Sinkhorn-Knopp introduces approximation error, though experiments show the deviation remains bounded. Results are demonstrated only on DeepSeek-V3's MoE architecture; generalization to dense models or other architectures remains unexplored. The memory overhead still scales with expansion rate n despite recomputation optimizations.
Check out the Paper. All credit goes to the researchers.
References
[1] Zhu, D. et al. (2024). Hyper-Connections. arXiv preprint. arXiv
[2] He, K. et al. (2016). Deep Residual Learning for Image Recognition. CVPR 2016. arXiv
[3] He, K. et al. (2016). Identity Mappings in Deep Residual Networks. ECCV 2016. arXiv
[4] DeepSeek-AI. (2024). DeepSeek-V3 Technical Report. arXiv preprint. arXiv
[5] Xiao, D. et al. (2025). MUDDFormer: Breaking Residual Bottlenecks via Multiway Dynamic Dense Connections. ICML 2025. arXiv
[6] Mak, B. & Flanigan, J. (2025). Residual Matrix Transformers: Scaling the Size of the Residual Stream. ICML 2025. arXiv
[7] Sinkhorn, R. & Knopp, P. (1967). Concerning Nonnegative Matrices and Doubly Stochastic Matrices. Pacific Journal of Mathematics. Link
[8] Vaswani, A. et al. (2017). Attention Is All You Need. NeurIPS 2017. arXiv
